1. Introduction
In the last decade, a new approach to smooth $4$-manifold topology has emerged from the intersection of categorified link homology, operad theory, and higher categories. Recent work of Morrison–Walker–Wedrich introduced the skein lasagna module $\mathcal S(W)$ of a $4$-manifold $W$: a combinatorial invariant built from Khovanov–Rozansky $\mathfrak{gl}_N$ homology.
What makes this construction striking is that it already distinguishes:
- orientation $\mathcal S(\mathbb{CP}^2) \neq \mathcal S(\overline{\mathbb{CP}^2})$,
- the topology of even vs. odd intersection forms ($\mathcal S(S^2 \times S^2) = 0$),
- and even exotic smooth pairs.
These are the kinds of phenomena previously visible only through analytical tools such as Donaldson theory or Seiberg–Witten theory.
The lasagna module achieves this using only:
- KR foams,
- surfaces and webs,
- local gluing rules,
- and $4$-ball fillings.
No analysis, no PDE, no gauge theory — just combinatorics and category theory.
This motivates a natural—and profound—question:
Does the lasagna module arise from a fully extended $4$-dimensional topological quantum field theory (TQFT) as classified by the Cobordism Hypothesis?
My emerging research program aims to answer yes, by constructing the final missing ingredient:
the full dualizability of the KR foam $2$-category inside an $(\infty,4)$-category.
This document outlines the plan, the mathematics behind it, and why this project matters.
2. Background: The Cobordism Hypothesis
The Cobordism Hypothesis was originally conjectured by Baez–Dolan (1995) and later (essentially) proven by Lurie (2009), with alternative frameworks by Ayala–Francis and Grady–Pavlov.
The statement (physics version):
An $n$-dimensional fully extended TQFT is completely determined by a single object
$$
Z(\mathrm{pt}) \in \mathcal C,
$$
provided this object is fully dualizable in the symmetric monoidal $(\infty,n)$-category $\mathcal C$.
Everything else —
lines, surfaces, 3-manifolds, 4-manifolds —
is generated from this one object by the higher-categorical duality operations encoded by the little disk operad.
The statement (precise version):
For a symmetric monoidal $(\infty,n)$-category $\mathcal C$,
$$
\mathrm{Fun}^{\lambda}
\otimes
(\mathrm{Bord})n^{\lbrace \mathrm{fr} \rbrace}(\mathcal{C})
\simeq
\mathrm{Obj}{\mathrm{fd}}(\mathcal{C})
$$
where $\mathrm{Obj}_{\mathrm{fd}}$ denotes the fully dualizable objects.
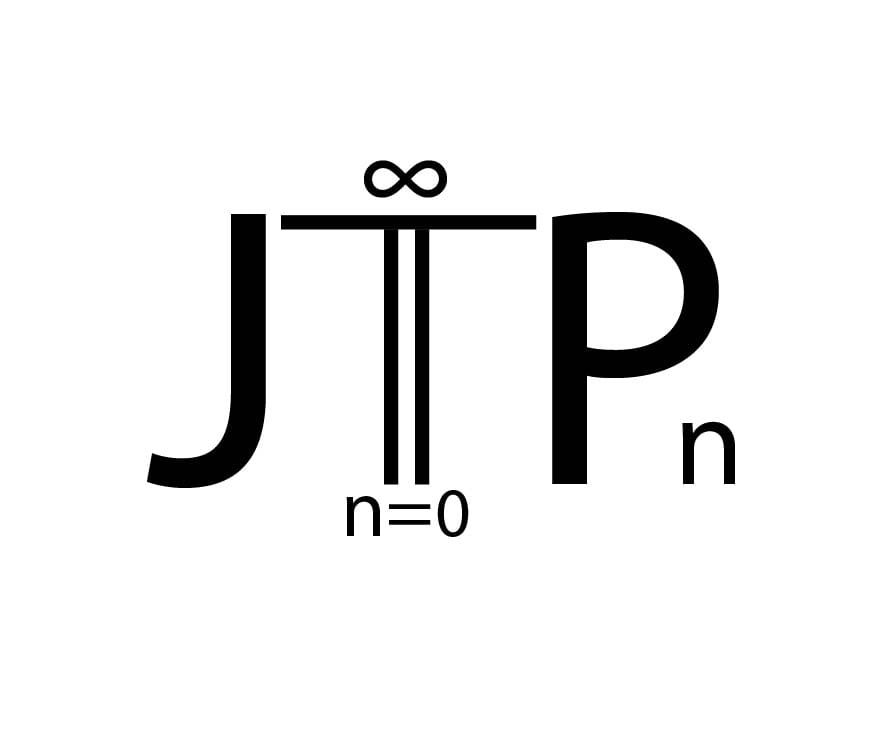
Thus, to define a fully extended $4$-dimensional TQFT, it suffices to exhibit a single fully dualizable object in a suitable $(\infty,4)$-category.
Why this matters
The hypothesis formalizes the idea that local data fully determines global topological data.
This is the same organizing principle behind:
- $E_n$-algebras,
- factorization homology,
- higher operads,
- and the stratified/recursively defined skein lasagna module.
The lasagna module looks and behaves exactly like the value on a point of a $(2+1+1)$-dimensional TQFT.
3. The Lasagna Module as a Candidate TQFT
Given a smooth, oriented $4$-manifold $W$, Morrison–Walker–Wedrich define a module
$$
\mathcal S_N(W;L)
$$
generated by lasagna fillings: surfaces and foams embedded in $W$ with local $\mathfrak{gl}_N$ Khovanov–Rozansky labels.
Key results so far:
1. Boundary compatibility
For any $2$-handlebody $W$ attached along a link $L$,
$$
\mathcal S_N(W) \cong KhR_N(L).
$$
So the lasagna functor recovers the categorified boundary invariant correctly.
2. Orientation detection
$$
\mathcal S_N(\mathbb{CP}^2) \not\cong
\mathcal S_N(\overline{\mathbb{CP}^2}).
$$
3. Exotic detection
There exist smooth, homeomorphic $4$-manifolds $X, X'$ such that
$$
\mathcal S_N(X) \not\cong \mathcal S_N(X').
$$
4. Trisection compatibility
Any closed $4$-manifold $X$ admits a trisection
$$
X = X_1 \cup X_2 \cup X_3
$$
where all pieces and their intersections are exactly the kinds of objects that lasagna fillings understand.
5. Operadic locality
A fundamental move:
$$
\text{Replace a 4-ball with its own lasagna filling.}
$$
This is precisely the structure of the framed little $4$-disks operad $E_4^{\mathrm{fr}}$.
All the ingredients of the Cobordism Hypothesis are present except one.
And this last missing piece is where I enter.
4. My Proposed Contribution
Goal:
Prove that the KR foam $2$-category $\mathcal F_N$ is a fully dualizable object in a suitable symmetric monoidal $(\infty,4)$-category.
If this is done, then by the Cobordism Hypothesis:
- the lasagna construction is a fully extended 4D TQFT,
- the module $\mathcal S_N(W)$ is the TQFT’s value on a closed $4$-manifold,
- and the theory becomes the first combinatorial, categorified 4D TQFT to detect exotic smooth structure.
The higher-categorical reason this is the final step is subtle:
Dualizability conditions (the roadmap)
To be fully dualizable in an $(\infty,4)$-category, $\mathcal F_N$ must have:
- object duals (0-dualizability),
- adjoints for all 1-morphisms (webs),
- adjoints for all 2-morphisms (foams),
- adjoints for 3-morphisms (foam cobordisms / movie moves),
- adjoints for 4-morphisms (lasagna fillings themselves).
The first layers are known or accessible; the higher layers require organizing foam relations and lasagna-substitution into a coherent adjoint-calculus.
This is a deep structural recursion problem.
It is exactly the kind of structure where my own mathematical style — recognizing self-similarity, recursion, and operadic closure — becomes an advantage.
5. Why This Would Be Significant
If successful, the result would produce:
1. The first combinatorial, categorified 4D TQFT that detects exotic smooth structure
Donaldson and Seiberg–Witten theories use analysis/PDE/gauge theory.
Lasagna theory uses webs and foams.
2. A new bridge between homological link invariants and smooth $4$-manifold topology
This would be as conceptually transformative as:
- Jones polynomial $\to$ Donaldson theory,
- Khovanov homology $\to$ categorified QFT,
- Floer homology $\to$ Heegaard–Floer theory.
3. A full $(2+1+1)$-dimensional TQFT
Not just a shadow of a TQFT, but an actual extended field theory with:
- values on points (KR 2-category),
- values on circles (foam bimodule categories),
- values on surfaces (cornered lasagna bimodules),
- values on 3-manifolds (boundary theories),
- values on 4-manifolds (lasagna module).
4. A new computational framework for smooth 4-manifolds
Trisections + categorified surface foams could become a new calculus for building and comparing $4$-manifolds.
This would open a computational frontier that was previously inaccessible.
6. Summary
My research program aims to complete the last conceptual step connecting:
- Khovanov–Rozansky homology,
- the skein lasagna module,
- trisections of 4-manifolds,
- little-disks operads,
- and the Cobordism Hypothesis.
The objective is:
To prove full dualizability of the KR foam $2$-category and thereby produce a fully extended, combinatorial 4D TQFT whose closed-manifold value is the lasagna module.
Given the recent smooth-structure detection results, this is a promising and mathematically natural direction — one that sits at the cutting edge of categorified topology, representation theory, and quantum field theory.

Discussion