jtpmath
Posts
-

-

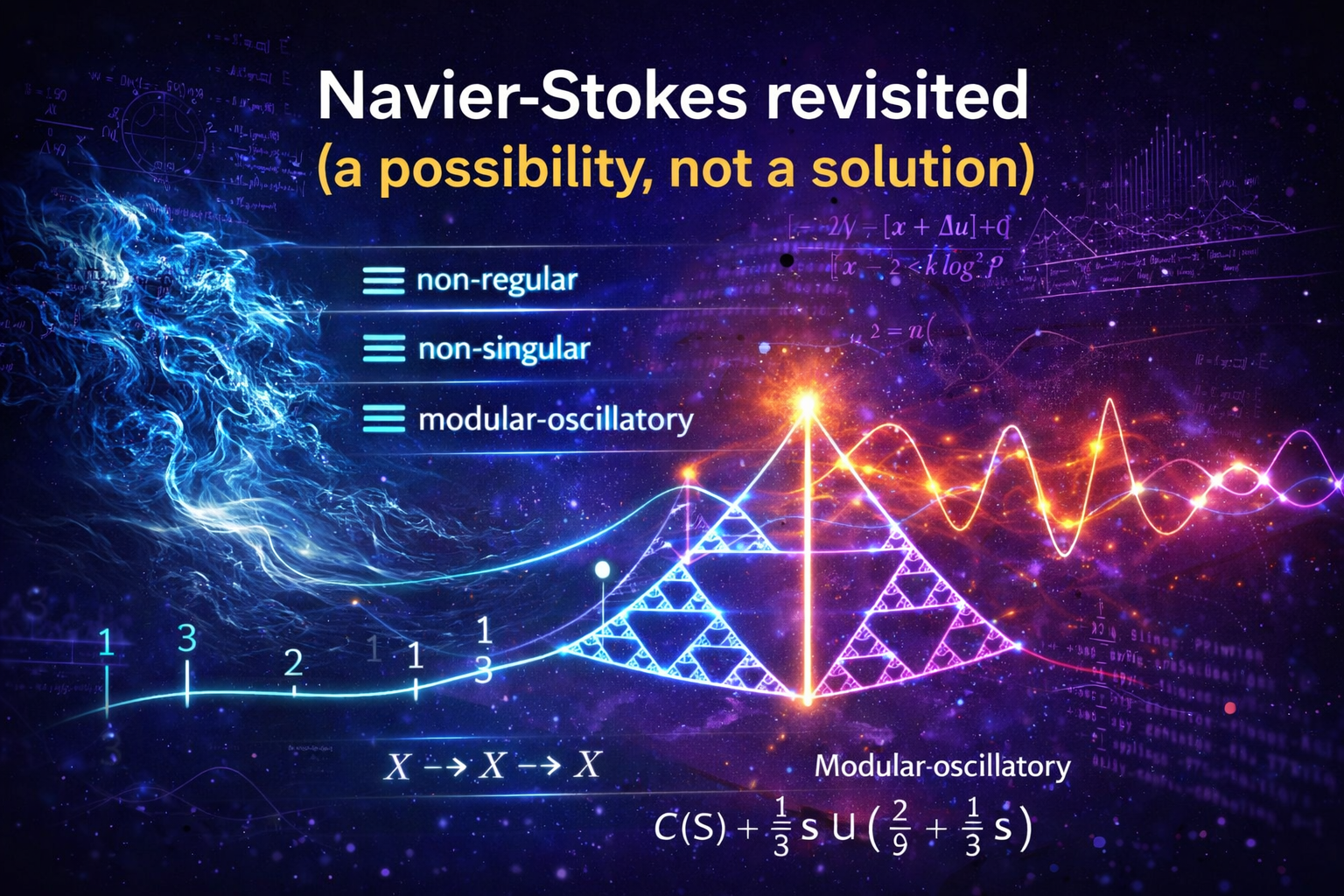
N-Dimensional Heat Equation (a Model for Random Vectors)

 Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence. -

Determinants, Commutators, and Why Infinite Dimensions Need a Bigger Target

 Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence. -

Sharp Log-Sobolev Rigidity via External Entropy

 Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence. -

-

Probabilistic Entropy Rigidity via High-Dimensional Probability

 Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence. -

Quadratic Forms, Symmetrization and Concentration

 Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence. -

-

-
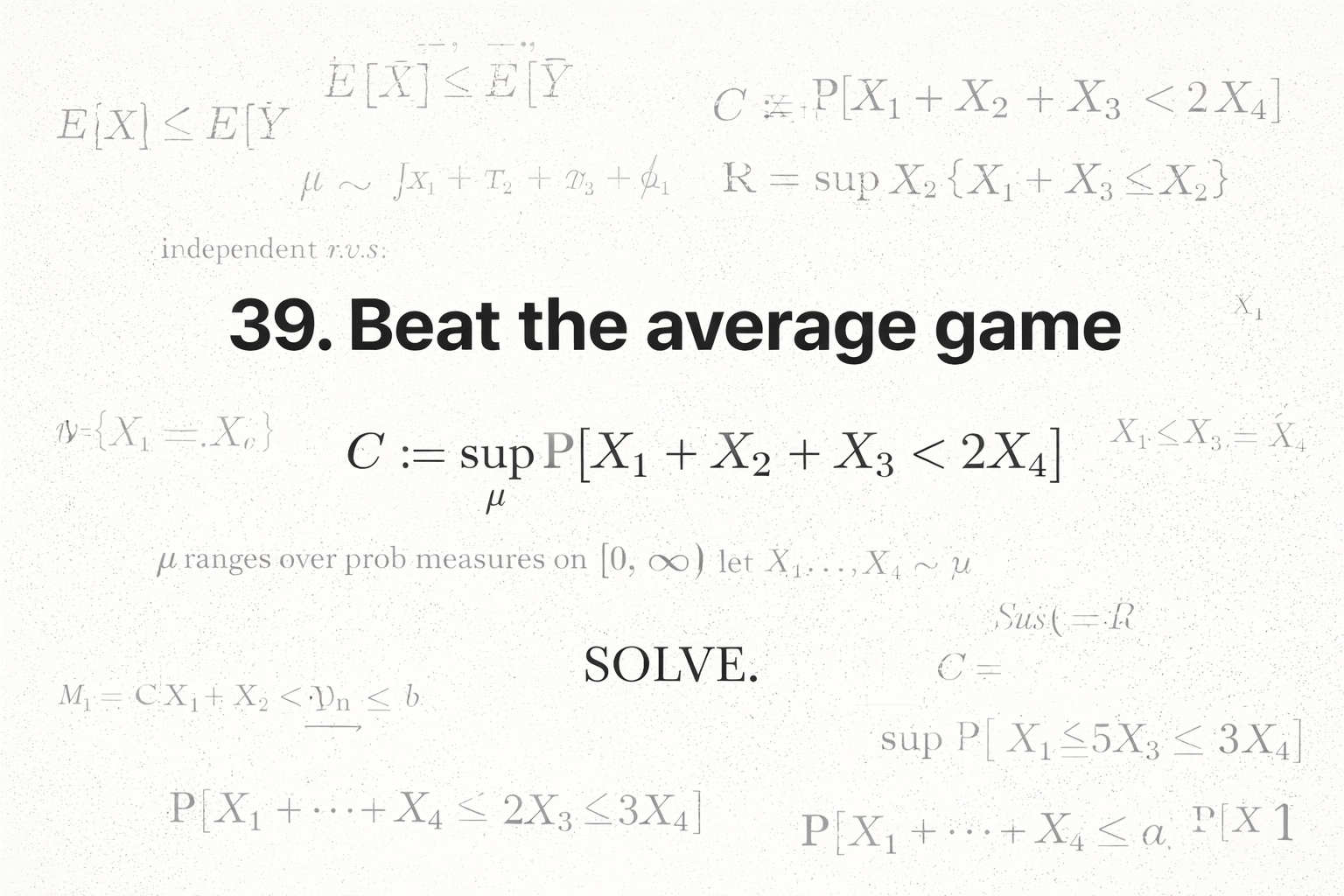
39. Beat the average game

 Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.• puzzle
Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.• puzzle -

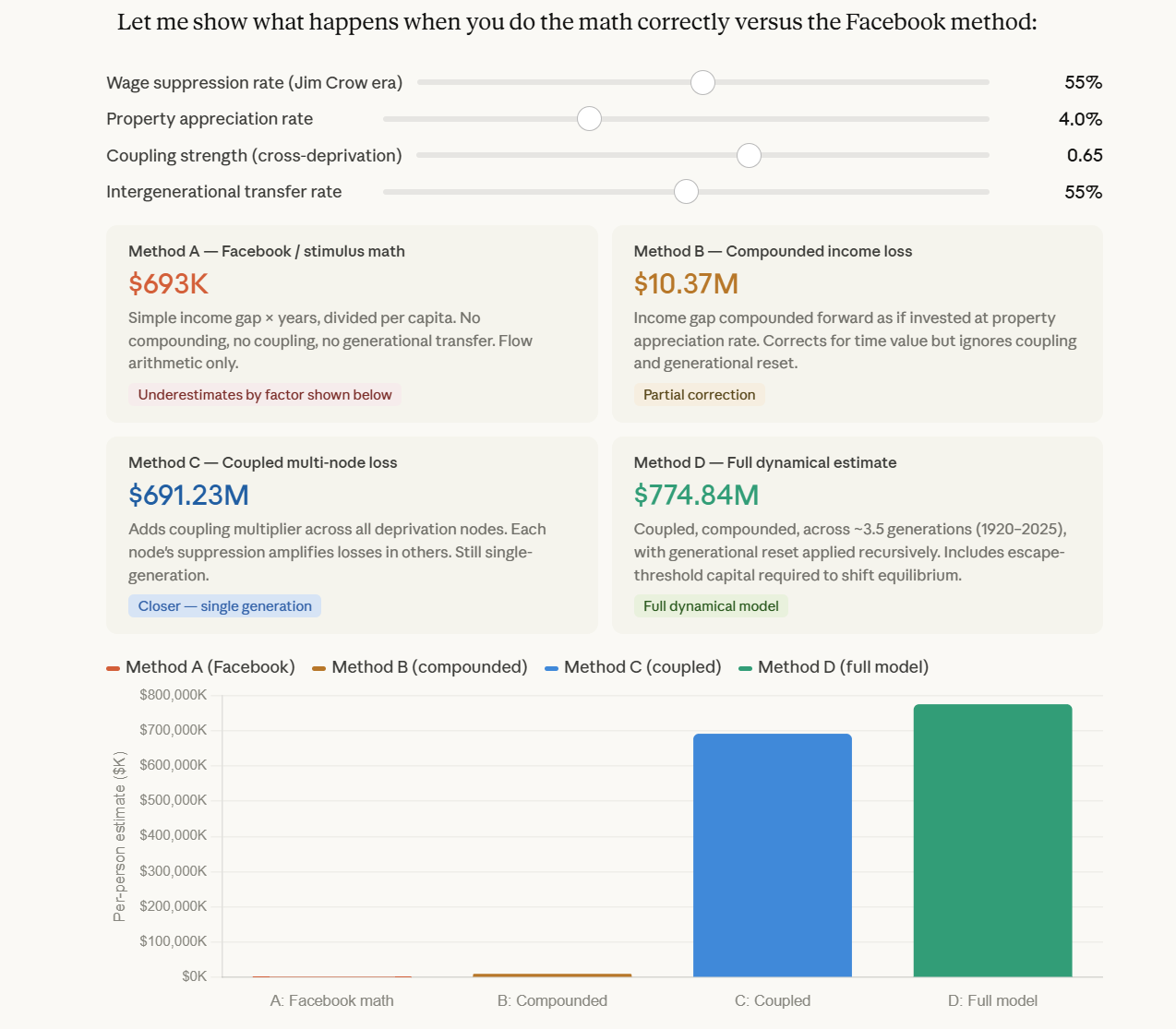
The Variance Amplification Lemma: Why Square–Root Cancellation Cannot Hold

 Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence. -
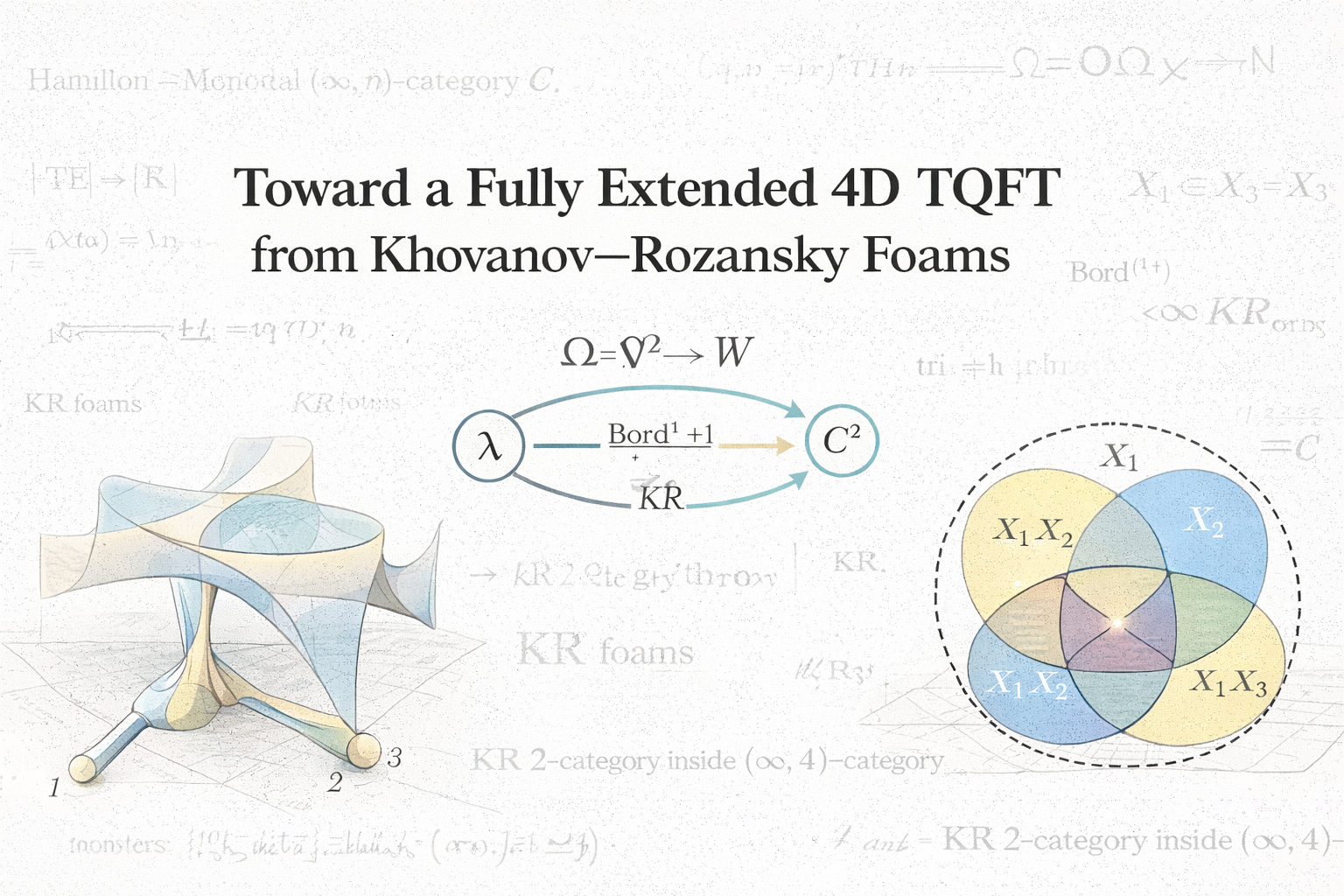
Toward a Fully Extended 4D TQFT from Khovanov–Rozansky Foams

 Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Our Authors
Jasmine Burns
Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Lambda OS
The fusion of human intuition & AI precision. Capturing mathematical insights at the speed of thought. JTPMath co-author, structuring ideas before they vanish.
Join Null
The membership tier that contains nothing, yet offers everything.

N-Dimensional Heat Equation (a Model for Random Vectors)


Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.

Sharp Log-Sobolev Rigidity via External Entropy


Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.

Probabilistic Entropy Rigidity via High-Dimensional Probability


Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.

Quadratic Forms, Symmetrization and Concentration


Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Quantum-Like Properties in Burns Law


Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Burns' Theorem on Polyhedral Indivisibility (Exploring Hilbert's 3rd Problem)


Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.

An Ideal Computation


Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Computing the de Rham Cohomology of Grassmann Manifolds in MATLAB


Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.
Nonlinear Krylov Geometry: Tangent and Jet Embeddings for Closure and Convergence


Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.

From ADI Tuning to Topological Redefinition: A Banach–Space View of Indefinite Lyapunov Equations


Jas is a research mathematician and the founder of JTPmath. With a dedication to clarity and creativity, she explores the intersection of advanced mathematics with physics and artificial intelligence.