Overview
Entropy rigidity results across dynamics and geometry share a common structure: an entropy bound, followed by a classification of equality cases, leading to algebraic or geometric rigidity. Traditionally, these results rely on homogeneous dynamics, representation theory, or deep measure classification theorems.
This post presents a probabilistic entropy rigidity template based on high-dimensional probability. The central idea is simple:
Entropy bounds arise from concentration; rigidity follows from equality in sharp concentration inequalities.
This framework unifies flat, curved, and evolving geometries using diffusion and quadratic energy models.
Tags:
- entropy rigidity
- dynamical systems
- high-dimensional probability
- Ricci flow
- concentration of measure
- Burns Law
JTPMath categories:
- Research Notes
- Probability & Geometry
- Dynamics summary: "A probabilistic template for entropy rigidity based on concentration inequalities, equality cases, and curvature-driven diffusion."









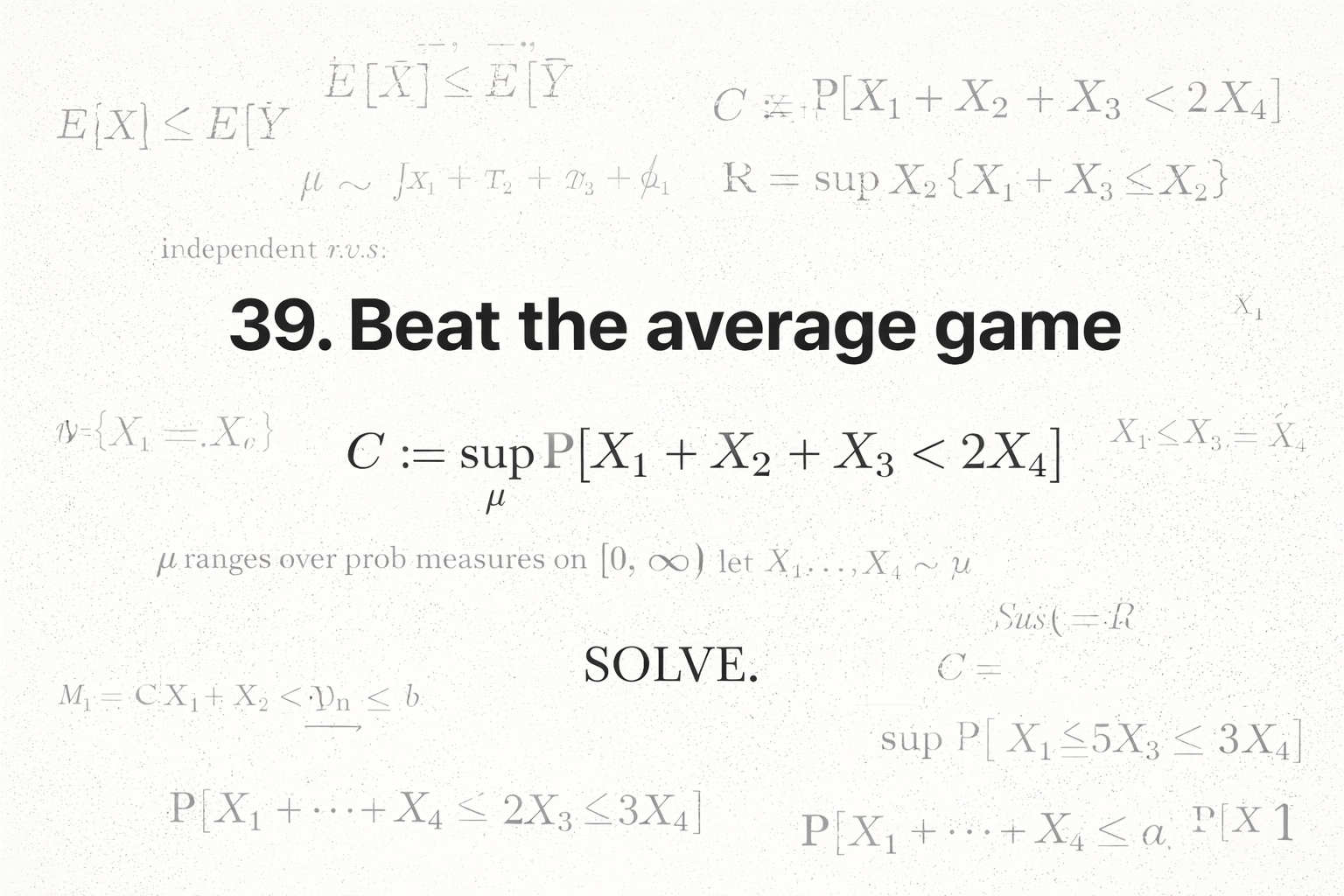


Discussion